Medical Physics in Radiation Oncology
- Imaging and Radiooncology

Prof. Dr. Oliver Jäkel
Head of the Division
Our division is performing innovative research and development in medical physics, in order to improve radiation therapy of tumor diseases. This includes image guided radiotherapy and based on this, the development of adaptive radiotherapy including modern AI-driven algorithms, i.e. for daily adaption of therapy. Another important research area is proton and ion beam therapy, where Heidelberg has a leading role, partially also due to our research.
Image: Example of a treatment plan in the pelvic region on a phantom to test the workflow of adaptive radiotherapy,
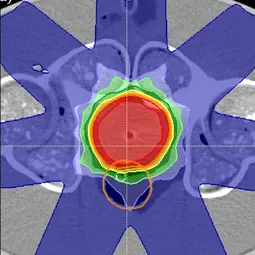
Image: Example of a treatment plan in the pelvic region on a phantom to test the workflow of adaptive radiotherapy,
Our Research
Our research focuses on physical methods used in radiation therapy in order to improve the therapy.
Present research priorities
The central research questions deal with image-guided therapy, i.e. the integration of daily anatomical images taken immediately before, or during therapy. For this purpose, both X-ray-based images (so-called Cone Beam CT) and MR images are used. The aim is to use these images to adapt the therapy on the respective treatment day (so-called adaptive therapy). These procedures enable us to optimally adapt the therapy to the actual anatomical situation and to spare healthy tissue. The tasks to be addressed, start with image processing (in particular tracking the anatomical structures, for which a so-called deformable image registration is necessary), in order to correctly take the actual anatomical conditions into account. This is followed by the recalculation and optimization of the dose based on clinical requirements, as well as the review of the radiation parameters (quality assurance) before they are used for the treatment. Since all steps are time-critical, the use of modern AI-based algorithms is essential.
All of the topics mentioned above are also being researched in our division for radiation therapy with proton and ion beams, which is becoming even more important due to the potentially higher accuracy of this treatment modality.
Our research topics are complemented by the development of novel measurement techniques that can be used for dosimetry and for the monitoring of therapy during irradiation. Radiobiological investigations of the effectiveness of proton and ion beams are also highly relevant, as they directly influence clinical strategies for the use of this therapy techniques.
Current developments
In close collaboration with the Clinical Cooperation Unit Radiotherapy at the DKFZ, we have developed and implemented a modular system for MR-guided radiotherapy (MARS) that is particularly suitable for the integration of functional MR imaging into adaptive therapy (Kim et al. 2024).
This system is being evaluated in several clinical trials, e.g. in a study on cervical cancer (Weykamp et al. 2024) or in the multicenter study we initiated to investigate the role of MR-guided radiotherapy for non-small cell lung tumors (PUMA Trial). One of the goals of this study is to use MR scans to determine during therapy whether patients are responding to the therapy or whether there are also early signals for the development of side effects.
In the field of ion beam therapy, a patient study as part of a clinical trial for the introduction of therapy with helium ions at the Heidelberg Ion Beam Therapy Center (HIT) was completed at the end of 2024. Here, we contributed to radiobiological studies on the effectiveness of helium ions and thus also to the precise measurement of the radiation dose (Hintz et. al 2022).
In a project on MR-guided therapy with ion beams (the ARTEMIS Project), we were able to make significant contributions in the field of dosimetry of ion beams in magnetic fields (Marot et al. 2023, Surla et al. 2024), dose calculation in magnetic fields (Burigo et al. 2022), the development of new methods for quality assurance and novel methods for patient positioning in an MRI scanner (Beyer et al. 2024). The ARTEMIS Project was funded by the Federal Ministry of Education and Research (FMER).
At the beginning of 2025, we also received a grant from the Carl Zeiss Foundation to develop the possibility of a completely new form of radiation therapy with miniaturized accelerators together with the Karlsruhe Institute of Technology (KIT). These accelerators are based on a physical mechanism recently discovered at KIT for accelerating electrons using laser light, which is based on structures that are only a few centimeters in size. This means that the ultra-compact electron accelerators might in the future be inserted into the body using minimally invasive endoscopy, where electron beams are then generated directly in the body close to the tumor. This would enable high-precision treatment while sparing healthy tissue (Ultracompact electron accelerators for internal radiotherapy (UCART)).
Methods and technologies
The methods we develop and use are based in particular on computer algorithms, especially in the area of therapy planning. New algorithms are developed and then tested in prototypes. Simulation codes (so-called Monte Carlo simulations) are an important tool, allowing us to examine in detail the physical interactions of radiation with matter in order to optimize the respective application.
Another major research area are algorithms based on artificial intelligence. These are mostly algorithms that help to automate and accelerate time-consuming tasks that usually have to be performed by hand. This requires large amounts of clinical data, which we obtain from clinical studies conducted by our partner institutes.
Many members of our division are physicists who come from the field of particle physics. We are therefore trying to use measurement systems from particle physics for applications in radiation therapy. One example of this is the MediPix detector, which is used in the so-called Large Hadron Collider (LHC) at Cern in Geneva, Switzerland. We use this detector for therapy monitoring and also to develop novel imaging with ion beams.
In recent years, we have also acquired extensive expertise in the field of rapid prototyping based on 3D printing processes. These are used in particular to develop realistic, dynamically variable body phantoms for various areas of the body. These so-called anthropomorphic phantoms are needed to test complex methods and algorithms for radiation therapy before they can be used clinically.
Finally, we have many years of expertise in conducting radiobiological investigations, which, in particular, enables us to compare the effects of ion beams with those of X-rays using various models. This is crucial for optimizing ion beam therapy.
Goals and societal relevance
Our work aims to further optimize radiation therapy and to adapt the treatment based on individual circumstances of each patient (so-called personalized oncology). In particular, daily anatomical changes are also taken into account. Furthermore, the radiation dose can be optimally adapted to the tumor volume in each case. This makes radiation therapy more precise and thus more tolerable and effective. In the long term, further clinical parameters and, for example, genomic data of each patient will also be included in this optimization. In this way, we are contributing to the further development of radiation therapy, which is one of the most important tools in oncological therapy. The development of ultra-compact internal radiation devices together with the KIT could help to ensure sustainable radiation therapy for tumor patients in less developed countries of the world as well.
Last but not least, we engage strongly in education and teaching as well as in outreach activities. This includes workshops and summer schools for students at all levels, postgraduate education and advanced trainings in radiation therapy and medical physics, as well as informing the general public in lectures and activities we organize for school classes, e.g. as part of the International Day of Medical Physics on 7 November every year.
Selected Projects
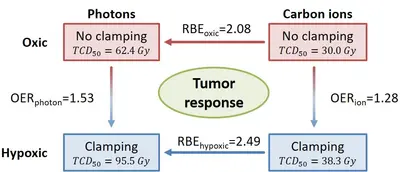
Project Name: High-, moderate- and low-LET ion beams in the treatment of radioresistant tumors: Impact of beam quality, tumor grading, and hypoxic status on radiation response.
Project Duration: 04/2020 - 01/2025 (2nd funding period)
Research Group: Applied Medical Radiation Physics (Head: Prof. Dr. Christian Karger)
Finanziert durch: Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 319589509
Besides allowing for highly conformal irradiations, ion beams also exhibit an increased radiobiological effectiveness (RBE), which may be suited to improve the effectiveness in the treatment of hypoxic tumors. This project investigates the RBE of experimental prostate tumors in the rat under normoxic (oxygen breathing) and hypoxic (clamping of tumor-supplying artery) conditions after irradiation with photons, protons, helium, carbon and oxygen ions and quantifies the oxygen enhancement ratio (OER). These investigations are accompanied by detailed histological characterization of the radiation response. See also Glowa et al. 2024 (DOI:10.1016/j.ijrobp.2024.05.004)
Click here for more details.

Project Name: matRad – an open-source dose calculation and treatment planning toolkit
Funding Period: 2022 – 2025
Research Group: Radiotherapy Optimization (Head: Dr. Niklas Wahl)
Funding Information: matRad development is currently funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) -- Project No. 443188743: "Sustainable development of the open source radiotherapy dose calculation and optimization toolkit matRad"
matRad is an open source software for radiation treatment planning of intensity-modulated photon, proton, and carbon ion therapy. matRad is developed for educational and research purposes and entirely written in MATLAB. matRad is published on GitHub (https://github.com/e0404/matRad) and is used in numerous in-house, collaborative, and independent international research projects.
matRad implements established dose calculation algorithms for photons, protons and carbon ions as well as non-linear constrained biological treatment plan optimization. It includes open patient and machine data and features a graphical user interface and a powerful scripting API. During the funding period, matRad will be extended to facilitate interfacing of open Monte Carlo dose calculation techniques, inclusion of helium and advanced biological models, and working with matRad from Python. Further, development will be professionalized to follow continuous integration standards and automated tests & builds.
Click here for more details.
Project Name: Online adaptive radiotherapy for locally advanced lung cancer: assessing the patient benefit in a multi-centric comparison of CBCT- and MRI-guidance approaches
Project Dauer: 03/2023 - 02/2028
Research Group: Advanced Image-Guided RadioTherapy (Head: Prof. Dr. Oliver Jäkel)
Funded by: German Cancer Aid, funding number 70114708 => 8. Ausschreibungsrunde (2021)
Within the Priority Program Translational Oncology of the German Cancer Aid, we were successful to obtain funds for a collaborative research project and clinical study for radiotherapy in lung cancer patients. For our project application entitled Online adaptive radiotherapy for locally advanced lung cancer: assessing the patient benefit in a multi-centric comparison of CBCT- and MRI-guidance approaches, we were able to obtain a 1.5M€ grant to perform a clinical trial for MR-guided radiotherapy, which has been initiated at the three participating MR-linac centers at the University Hospitals in Heidelberg, Tübingen and the Ludwigs-Maximilians-University (LMU) in Munich and which will soon be started at the new ETHOS® system at DKFZ.
Click here for more information.
You can find an overview of selected research projects of our division here.
You can also find further research projects on the websites of our research groups.
Team
Our team consists of around 60 - 70 people, organized into eight research groups. Together with their group leaders, each group consists of Bachelor's, Master's and PhD students as well as Post-Docs with backgrounds in medical physics, medical technology, computer science or other related disciplines. There is also a team for further education and training in the field of medical physics.
- Show profile

Prof. Dr. Oliver Jäkel
Head of the Division
-

Margit Dietz
Secretary of the Division
-

Prof. Dr. Christian Karger
Research Group Leader of E0402
-

Dr. Niklas Wahl
Research Group Leader of E0404
-

Armin Runz
Research Group Leader of E0405
-
Dr. Peter Haering
Research Group Leader
-

Wibke Johnen
Deputy Research Group Leader of E0405
-

Dr. Maria Martisikova
Research Group Leader of E0406
-

Dr. Tim Gehrke
Deputy Research Group Leader of E0406
-

Dr. Jose Alberto Vedelago
Research Group Leader of E0408
-

Dr. Simone Barthold-Beß
Scientific Officer
-

Anna Moshanina
Office Administration "Further Education and Training"
-

Marcel Schäfer
Program and E-Learning Coordinator "Further Education and Training"
Research Groups
Doctorate, Further Education and Training, Events

Doctorate in Medical Physics at DKFZ
The DKFZ has its own multidisciplinary research program with a focus on “Imaging and Radiation Oncology”. This research program is concerned with the introduction of new findings, methods and technologies for the diagnosis and treatment of cancer.
Further Education and Training in Medical Physics
Our division offers various online-based courses and continuing education programs. These are aimed at students and young scientists, as well as experienced professionals with several years of practical experience in clinics or research institutions.

Events
For many years, our division organizes various events in the field of medical physics and radiotherapy together with national and international partner institutions. Furthermore, we host the regular seminar “Medical Physics” together with the Division of Medical Physics in Radiology, taking place during the summer and winter term.
Selected Publications
Kelleter L, Marek L, Echner G, Ochoa-Parra P, Winter M, Harrabi S, Jakubek J, Jäkel O, Debus J, Martisikova M.
Cristoforetti R, Hardt JJ, Wahl N.
Glowa C, Saager M, Hintz L, Euler-Lange R, Peschke P, Brons S, Hilt K, Friedrich T, Scholz M, Liew H, Mairani A, Karger CP
Katseena Yawson A, Sallem H, Seidensaal K, Welzel T, Klüter S, Maria Paul K, Dorsch S, Beyer C, Debus J, Jäkel O, Bauer J, Giske K.
Stengl C, Christensen JB, Muñoz ID, Neuholz A, Brons S, Yukihara EG, Liermann J, Jäkel O, Vedelago J.
Schlegel W, Karger CP, Jäkel O. (Hrsg.)
Awards
Heidelberg Institute for Radiation Oncology (HIRO)
Our division is member of the Heidelberg Institute for Radiation Oncology (HIRO).

Get in touch with us


